Activity 5-A - Familiarization with Discrete FFT
Using the 2-dimensional discrete fast fourier transform (FFT) function of Scilab which is fft2, we are familiarized with what it does when applied to images.
The first set of pictures shown below illustrates the result of discrete FFT in an image. Initially, a 128x128 image of a white circle which is leftmost picture with black background is made in Paint. The image is then read and converted to grayscale-type where fft2 is applied. The effect of fft2 to the circle is represented by the second image. The third one shows the result when the function fftshift is used on the second image. The rightmost image illustrates the inverse FFT of the FFT of the first image equivalently applying fft2 twice.
It is important that the FFT images are applied by the abs function which computes the modulus of complex numbers that fft2 returns and so it will give intensity values.
The second picture is the effect of the first application of fft2 since the white circle is divided into four being distributed on the four quadrant corners. The third one represents an image of airy disks which is the consequence of fftshift. This produces the diffraction pattern of a circular aperture where Fourier Transform is involved. The pattern is more apparent because I have made a small circle. Finally, when fft2 is used twice on the first image, it comes back to its original form knowing actually it is already inverted but of course is not obvious here since the object is a circle.
For other illustrations of the functions fft2, fftshift and the inverse FFT on an image, a white letter A is created with black background again in Paint. The following images summarize the result.
The first one is the original created image. The second is the first fft2 aplication. Next is the fftshifted image of the second and the last one illustrates the inverse FFT which indeed inverts the original image.
The Scilab code below is utilized for Activity 5-A.
// DFFT Circle, 5-A
I = imread('circle_paint.bmp');
Igray = im2gray(I);
FIgray = fft2(Igray);
//scf(0);
circlefft = abs(FIgray);
//imshow(circlefft, []);
//imwrite(circlefft/max(circlefft), 'circlefft.bmp');
//scf(1);
circlefftshift = fftshift(abs(FIgray));
//imshow(circlefftshift, []);
//imwrite(circlefftshift/max(circlefftshift), 'circlefftshift.bmp');
//scf(2);
circleifft = abs(fft2(fft2(Igray)));
//imshow(circleifft, []);
//imwrite(circleifft/max(circleifft), 'circleifft.bmp');
// DFFT Letter A, 5-A
a = imread('A.bmp');
Agray = im2gray(a);
A = 1 - Agray;
//imwrite(A, 'Ainv.bmp')
FAgray = fft2(A);
//scf(3);
Afft = abs(FAgray);
//imshow(Afft, []);
//imwrite(Afft/max(Afft), 'Afft.bmp');
//scf(4);
Afftshift = fftshift(abs(FAgray));
//imshow(Afftshift, []);
//imwrite(Afftshift/max(Afftshift), 'Afftshift.bmp');
//scf(5);
Aifft = abs(fft2(fft2(A)));
//imshow(Aifft, []);
//imwrite(Aifft/max(Aifft), 'Aifft.bmp');
Activity 5-B - Simulation of an Imaging Device
This next part involves convolution which can simulate an imaging device. Here, a circular aperture is used. VIP with large Arial font is created in Paint. The rightmost image below illustrates the consequence of convolution on the circular aperture and VIP.
It can be observed above that the convolved image is inverted and not clear. The inversion of VIP is due to the application of inverse FFT to the convolution. The aperture is small hence the object is not well-reconstructed.
Now, let's see the effect of a larger radius circular aperture.
Obviously, VIP is still inverted but it is now clearer than the previous aperture. However, the intensity is not the same as the original VIP which proves that the reconstruction in imaging systems is not perfect.
The Scilab code below is utilized in this part.
// Convolution 5-B
vip = imread('vip.bmp');
c = imread('circle_paint.bmp');
cgray = im2gray(c);
vipgray = im2gray(vip);
Fr = fftshift(cgray);
Fvip = fft2(1 - vipgray);
//imwrite(1 - vipgray, 'vipgrayinv.bmp');
FRA = Fr.*(Fvip);
IRA = fft2(FRA); //inverse FFT
FImage = abs(IRA);
//scf(7);
//imshow(FImage, []);
//imwrite(FImage/max(FImage), 'Aconv.bmp');
Activity 5-C - Template Matching using Correlation
The third part matches a particular letter in a sentence using correlation. The image of a sentence at the leftmost side shown below is created in Paint. This has an Arial font and written in capital letters. Next, an image for letter A which is the second image below is made considering that it is also capitalized and has the same font type and size as used in the sentence. Correlation works when the Fourier transform of the letter A image is multiplied element-by-element to the conjugate of the Fourier transform of the text image. Then, the inverse FFT is applied.
The third image illustrates the correlated image of the text. It can be observed that the letter A's of the text have bright spots which indicate the letter A is indeed matched with the text using correlation. The similarity of the font type and size of letter A is very important for better correlation so that the Fourier transform of A best matches the incidence of this same transform from the text.
The Scilab code below is utilized in Activity 5-C.
// Correlation 5-C
rain = imread('rain.bmp');
a_rain = imread('a_rain.bmp');
raingray = im2gray(rain);
a_raingray = im2gray(a_rain);
rainf = fft2(1 - raingray);
//imwrite(1 - raingray, 'raingrayinv.bmp');
a_rainf = fft2(1 - a_raingray);
//imwrite(1 - a_raingray, 'a_raingray.bmp');
correlate = abs(fftshift(fft2(a_rainf.*(conj(rainf)))));
//scf(8);
//imshow(correlate, []);
//imwrite(correlate/max(correlate), 'correlate.bmp');
Activity 5-D - Edge Detection using the Convolution Integral
The last part has the same algorithm as in the previous part but this time a special function in Scilab which is imcorrcoef is used and edges are matched here with a given pattern. Again, the image of VIP is used for edge detection. Different edge patterns which are 3x3 matrix are created for matching with VIP. It is important the sum of the matrix elements is equal to zero. The activity suggested the edge patterns to be used involve horizontal, vertical and spot edge pattern. These are shown as follows which are arranged respectively.
The set of images below illustrates the result of edge detection.
The first image is the original VIP. Next is the result of a horizontal edge pattern which makes the vertical edges to disappear and generates horizontal bright stripes. The third is based from a vertical edge pattern apparently producing vertical stripes and removing horizontal edges. The last image uses a spot edge pattern where no edges are erased instead they are brightly highlighted.
The Scilab code below is utilized in this last part.
// Edge Detection 5-D
pattern1 = [-1 -1 -1; 2 2 2; -1 -1 -1];
pattern2 = [-1 2 -1; -1 2 -1; -1 2 -1];
pattern3 = [-1 -1 -1; -1 8 -1; -1 -1 -1];
vip_edge = imcorrcoef(1 - vipgray, pattern3);
//imshow(vip_edge/max(vip_edge));
//imwrite(vip_edge/max(vip_edge), 'vip_edge3.bmp');
Because I have successfully fulfilled all the objectives and procedures to each part of this activity, I grade myself 10/10.
This activity is completed through collaborating with Gary and Raffy.


















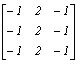





No comments:
Post a Comment