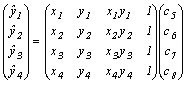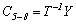Activity 15 - Probabilistic Classification

This activity is similar to the previous one except that another method is implemented here. Objects are grouped here using probabilistic classification.

Instead of 3, only 2 classes are considered here which are all from Activity 14, Snacku rice crackers and Superthin biscuits. As assembled previously, 10 samples represent each class. These are shown below.

Also, the 4 features which are the sample's pixel area, normalized chromaticity values in red, green, and blue and their corresponding data from Activity 14 are used for probabilistic classification. Each class is again divided into a training set and a test set where each set contains 5 samples.
The probabilistic classification is rooted from the algorithm of linear discriminant analysis (LDA). From the following discriminant function, a test object k is assigned to class i that has maximum f_i.

Note that the transpose matrix operation is represented by T and -1 is the inverse matrix operation. The last term contains the prior probability of class i shown below.

From the equation above, n_i is the number of samples in class i and N is the total number of samples in the training set. Meanwhile, matrix C is called the pooled within class covariance matrix and this obtained from matrix c which is called the covariance matrix. These are as follows.

Note that there are g total number of classes. Covariance matrix is determined from the mean corrected data and the features of the training set which are represented by the following expressions from top to bottom respectively.

The global mean vector mu consists the average of each feature w_i,j,m coming from all classes of the training set and M is the total number of features. Going back to the discriminant function f_i, mu_i is composed of the mean of each feature just from class i in the training set. Thus, using LDA to classify an unknown or test sample, a training set is still required in order to establish the discriminant function which categorize the test sample with the same features possessed by the training set to a class.

The table below summarizes the data gathered from the training set (click the table for larger view).

Finally, the results of the LDA to the test set are summarized in the following table (click the table for larger view).

It can be observed that the values between the two discriminant functions are very small for all samples of the test set compared to the large deviations between the minimum distances acquired in Activity 14. The large values of discriminant function are because of the quantified feature pixel area which is relatively greater than the normalized chromaticity values. Nevertheless, all 10 samples of the test set are correctly grouped to their respective classes.

I grade myself 10/10 in this activity because I have implemented LDA properly and grouped all test samples to their expected classes.

I have successfully finished the activity individually. However, I have helped my classmates on how to handle this activity.

Appendix
The whole Scilab code below is utilized in this activity.

snacku_training = fscanfMat('snacku_training.txt');
superthin_training = fscanfMat('superthin_training.txt');
snacku_test = fscanfMat('snacku_test.txt');
superthin_test = fscanfMat('superthin_test.txt');

x_training = [snacku_training; superthin_training];
x_test = [snacku_test; superthin_test];

myu1 = [mean(snacku_training(:,1)), mean(snacku_training(:,2)), mean(snacku_training(:,3)), mean(snacku_training(:,4))];
myu2 = [mean(superthin_training(:,1)), mean(superthin_training(:,2)), mean(superthin_training(:,3)), mean(superthin_training(:,4))];

myu = [mean(x_training(:,1)), mean(x_training(:,2)), mean(x_training(:,3)), mean(x_training(:,4))];

x01 = [snacku_training(1,:) - myu; snacku_training(2,:) - myu; snacku_training(3,:) - myu; snacku_training(4,:) - myu; snacku_training(5,:) - myu];
x02 = [superthin_training(1,:) - myu; superthin_training(2,:) - myu; superthin_training(3,:) - myu; superthin_training(4,:) - myu; superthin_training(5,:) - myu];

n1 = 5;
n2 = 5;

c1 = (x01'*x01)/n1;
c2 = (x02'*x02)/n2;

for r = 1:4
for s = 1:4
C(r, s) = (n1/(n1 + n2))*(c1(r, s) + c2(r, s));
end
end

invC = inv(C);

P1 = n1/(n1 + n2);
P2 = n2/(n1 + n2);
P = [P1; P2];

for k = 1:(n1 + n2)
f1(k) = myu1*invC*x_test(k,:)' - (1/2)*myu1*invC*myu1' + log(P(1));
f2(k) = myu2*invC*x_test(k,:)' - (1/2)*myu2*invC*myu2' + log(P(2));
end

f = [f1, f2];
//fprintfMat('f_test.txt', f);

class = [];
for i = 1:(n1 + n2)
[a, b] = find(f(i,:) == max(f(i,:)));
class = [class; b];
end

Activity 14 - Pattern Recognition

The main objective of this activity is to classify various objects with different characteristics through pattern recognition.

In pattern recognition, the characteristics of an object belonging to a type or class are called features. These are quantified which may be the object's area, color, and many others. Pattern is then a set of features and a class is a set of patterns which share common features. The task is thus finding the features of an unknown object belonging to one of the several classes.

There are 3 classes assembled in this activity. They are all edible which include Snacku rice crackers, Superthin biscuits, and Nova multigrain snack. Each class is composed of 10 samples. The setup is shown below.

The 30 samples are grouped according to their respective classes for simplified image processing. Each class is divided into two, 5 samples serve as the training set and the other 5 correspond to the test set. Features that have been decided to use for pattern recognition are the sample's pixel area, average normalized chromaticity values in red, green, and blue for a total of 4.
The pixel area is attained by binarizing and inverting the cropped image of a class using the most appropriate predetermined threshold value. The funciton bwlabel of Scilab is then implemented to sum up the white pixels of each cluster equivalent to the pixel area of a sample and this is similar to the algorithm in Activity 9.
Meanwhile, parametric segmentation in Activity 12 is employed to get the normalized chromaticity values in red, green, and blue of each sample. This is operated through cropped individual sample images of each class. Note that the normalized chromaticity values in red, green, and blue are ensured that these just came from the samples (not with the background) by extracting the pixel coordinates of the segmented images.
Next, quantified features are ordered into a matrix called feature vector. Hence, in this case, a sample's feature vector consists 4 elements. Mean feature vectors representing each class are then obtained using the following equation.

Here, N_j is the total number number of samples in a class w_j which is here, equal to 5 while the 1 x 4 matrix x_j is composed of all 4 feature vectors acquired from image processing and then this is summed for N_j samples. Through minimum distance classification stated by the following expression, the features of each sample in the test set is then compared to the matrix of mean features m_j in the training set.

From the expressions above, x is the feature vector of a test sample, W is the total number of class and T is the transpose matrix operation. The class index j of the minimum distance D_j(x) is then assigned to the Nth sample from the test set of a class.

The results from the training set are shown in the table below (click the table for larger view).

Finally, the resulting classification of the test set is summarized in the following table (click the table for larger view).

It can be observed that the calculated distance D_j(x) is relatively large when a test sample does not match the expected class. Notice that the distances are big numbers because recall that the quantified feature pixel area is relatively larger than the normalized chromaticity values. But most importantly, all 15 samples in the test set are classified correctly.

Since I have understood the process of pattern recognition using the minimum distance classification and at the same time, successfully classifying all the samples in the test set, I grade myself 10/10 in this activity.

I have successfully completed this activity through discussions with Gary.

Appendix
The whole Scilab code below is utilized in this activity.

stacksize(4e7);

//snacku = gray_imread('snacku.jpg');

//scf(0);
//imshow(snacku);
//imwrite(snacku, 'gray snacku.bmp');

snack_A = [];
for a = 1:3
snack = gray_imread('gray snack'+string(a)+'.bmp');

if a == 1
snack = im2bw(snack, 175/255);
elseif a == 2
snack = im2bw(snack, 160/255);
else
snack = im2bw(snack, 155/255);
end

snack = 1 - snack;

//scf(a);
//imshow(snack);

[L, n] = bwlabel(snack);

A = [];
for i = 1:n
b = (L == i);
A(i) = sum(b);
snack_A(i, a) = A(i);
end

end

snacku_A = snack_A(:,1);
superthin_A = snack_A(:,2);
nova_A = snack_A(:,3);

training_snack_A = [snacku_A(1:5), superthin_A(1:5), nova_A(1:5)];
test_snack_A = [snacku_A(6:10), superthin_A(6:10), nova_A(6:10)];

// Average Normalized RGB Values

mean_snacku_r = [];
mean_snacku_g = [];
mean_snacku_b = [];
for j = 1:10
image = imread('snacku'+string(j)+'.jpg');
I = imread('snacku ROI.jpg');

R = I(:,:,1);
G = I(:,:,2);
B = I(:,:,3);

RGB = R + G + B;

r = R./RGB;
b = B./RGB;
g = G./RGB;

Ri = image(:,:,1);
Gi = image(:,:,2);
Bi = image(:,:,3);

RGBi = Ri + Gi + Bi;

ri = Ri./RGBi;
bi = Bi./RGBi;
gi = Gi./RGBi;

// Parametric Segmentation

rmean = mean(r);
gmean = mean(g);
rsigma = stdev(r);
gsigma = stdev(g);

rp = (1/(rsigma*sqrt(2*%pi)))*exp(-((ri - rmean).^2)/(2*rsigma^2));
gp = (1/(gsigma*sqrt(2*%pi)))*exp(-((gi - gmean).^2)/(2*gsigma^2));

rgp = round(rp.*gp);

//scf(j + 3);
//imshow(rgp);

[x, y] = find(rgp ~= 0);

snacku_r = [];
snacku_g = [];
snacku_b = [];
for k = 1:length(x)
snacku_r = [snacku_r, ri(x(k), y(k))];
snacku_g = [snacku_g, gi(x(k), y(k))];
snacku_b = [snacku_b, bi(x(k), y(k))];
end

mean_snacku_r(j,:) = mean(snacku_r);
mean_snacku_g(j,:) = mean(snacku_g);
mean_snacku_b(j,:) = mean(snacku_b);

end

training_mean_snacku_r = mean_snacku_r(1:5);
training_mean_snacku_g = mean_snacku_g(1:5);
training_mean_snacku_b = mean_snacku_b(1:5);
training_color_snacku = [mean(training_mean_snacku_r), mean(training_mean_snacku_g), mean(training_mean_snacku_b)];
//fprintfMat('training_color_snack1.txt', training_color_snacku);

test_mean_snacku_r = mean_snacku_r(6:10);
test_mean_snacku_g = mean_snacku_g(6:10);
test_mean_snacku_b = mean_snacku_b(6:10);
test_color_snacku = [test_mean_snacku_r, test_mean_snacku_g, test_mean_snacku_b];
//fprintfMat('test_color_snack1.txt', test_color_snacku);

// Test Object Classification

D_test_snack = [];
for l = 1:3
for m = 1:3
training_color_snack = fscanfMat('training_color_snack'+string(l)+'.txt');
m_snack = [mean(training_snack_A(:,l)), training_color_snack];

test_color_snack = fscanfMat('test_color_snack'+string(m)+'.txt');

for n = 1:5
x_snack = [test_snack_A(n, m), test_color_snack(n, 1), test_color_snack(n, 2), test_color_snack(n, 3)];
D_test = [x_snack - m_snack];
D_test_snack = [D_test_snack; sqrt(D_test*D_test')];
end

end

end

D_test_snacku = D_test_snack(1:15);
D_test_superthin = D_test_snack(16:30);
D_test_nova = D_test_snack(31:45);

D = [D_test_snacku, D_test_superthin, D_test_nova];

class = [];
for o = 1:15
[a, b] = find(D(o,:) == min(D(o,:)));
class = [class; b];
end

Activity 13 - Correcting Geometric Distortion

The barrel geometric distortion in an image is removed in this activity based on the image's pixel coordinates and graylevel values.

The following distorted image of a grid is obtained from the internet.

Source: http://www.jmg-galleries.com/blog/2007/08/01/photo-term-series-post-13-barrel-distortion

The correction starts with the image's pixel coordinates. A subgrid from a distorted image can be thought of transformation of this subgrid from the ideal image through functions in the horizontal and vertical coordinates as shown below.

The transformation of a vertex from a subgrid is then illustrated as follows.

The following transformation functions are thus bilinear if the vertex from the ideal image is mapped simultaneously in both directions.

Eight equations are enough to determine the unknown eight coefficients c_1 to c_8 and these come from the two coordinates of the four vertices of a closed region in the grid both in the distorted and ideal image. Hence, a different set of coefficients is yielded for other closed region.

Initially from the distorted image obtained from the internet, a vertex from the most undistorted region is located. In this case, it is approximately near the image's center. Then, the length in pixels of the ideal rectangle is measured. The size of the ideal rectangle in the grid is found to be 28 x 28 pixels. Starting from the vertex, the pixel coordinates by counting 28 pixels to its left, right, top and bottom are determined and so the vertex points of the ideal grid are generated which is shown as follows.

Notice that the pixel coordinates at the edges are also obtained in order to cover the whole distorted image in correcting the barrel distortion. Meanwhile, the pixel coordinates of the vertices in the distorted image corresponding to the ideal image are gathered using the function locate of Scilab.
The sets of coefficients for each rectangle are then determined from the following equations.

The matrix expressions can be rewritten as follows.

So the coefficients are computed as shown below.

Now, per pixel inside a rectangle, the coordinates from the distorted image are attained using the corresponding set of coefficients in that rectangle through the following equations.

The grayscale values of each pixel are the next to be handled. At first, a matrix of zeros with the same size of the distorted image (150 x 151) is created. Then, interpolated graylevel values of each computed locations in the distorted image are copied to this blank matrix.
Two types of graylevel interpolation are implemented here. The first one is the nearest neighbor interpolation technique where the graylevel value of the nearest integer-valued coordinate is used and this just comes from the rounded pixel coordinates in the distorted image calculated using the eight coefficients.
Bilinear graylevel interpolation is the second technique employed to correct the barrel distortion. Since many of the computed pixel coordinates in the distorted image are not integer-valued, this technique is expected to result to a better corrected image compared to the nearest neighbor graylevel interpolation. Otherwise, the graylevel value at integer-valued locations is automatically copied to the blank matrix. An illustration of bilinear graylevel interpolation is shown below.

The pixel location pointed above is clearly not integer-valued. Through the equation below, the graylevel value is obtained at this location.

Notice that the equation above has form exactly the same in calculating the pixel coordinates in the distorted image. Thus, the same procedure applies in the bilinear graylevel interpolation which is based from the matrix expression shown as follows.

The coefficients a, b, c, and d must first be determined using four equations. These are then coming from the four nearest pixels of each computed pixel coordinate in the distorted image. The integer coordinates are assumed to be at the center of each pixel hence the four nearest pixels are located at the rounded values of 0.5 pixel away from calculated pixel location in the distorted image for both directions. The 4 x 4 matrix from the expression above are then assembled for each computed pixel coordinate in the distorted image which contains the location of the four nearest pixels. The following is the simplified version of the matrix expression above.

Then, the coefficients a, b, c, and d for each computed pixel location in the distorted image are acquired as shown below.

The interpolated graylevel value of each calculated pixel location in the distorted image is then transferred to the blank matrix for each pixel inside a rectangle in the ideal grid. The whole algorithm is repeated for the other rectangles in the ideal grid.
Recall that vertices at the perimeter of the ideal grid and distorted image are also considered. Thus to prevent incorrect indexing, the graylevel value is directly copied from the distorted image onto the black matrix at the pixel coordinate inside a rectangle in the ideal grid, if the calculated pixel location is less than 1 or greater than the length of the image which is 150 for the vertical direction and 151 for the horizontal direction.

The next figure is the result of the nearest neighbor graylevel interpolation technique applied to the barrel distorted grid image.

It can be observed that the lines are pixelated and jagged even though the curved grid lines are straightened.
Meanwhile, the figure below is the result of the bilinear graylevel interpolation.

Apparently, bilinear graylevel interpolation is better than the nearest neighbor interpolation technique. The barrel distortion is completely eliminated at the same time producing smooth grid lines.

I say that this activity has the most complicated code so far but since I have successfully corrected the barrel distortion of a grid image and understand how the whole process is implemented, I grade myself 10/10.

Earl has helped me in this activity and I thank Mandy for explaining how she has implemented the bilinear graylevel interpolation technique.

Appendix
The following Scilab code is utilized in this activity.

stacksize(4e7);

distort = gray_imread('barrel_distortion.jpg');

pixelx = 28;
pixely = 28;
tran = 20;

s = size(distort);
ideal = zeros(s(1), s(2));

xit = [];
yit = [];
for i = 1:5
for j = 1:5
xit = [xit, tran + pixelx*(j - 1)];
yit = [yit, tran + pixely*(i - 1)];
ideal(tran + pixelx*(i - 1), tran + pixely*(j - 1)) = 1;
end
end

xit = matrix(xit, 5, 5);
yit = matrix(yit, 5, 5);

xi = zeros(7, 7);
yi = zeros(7, 7);
xi(2:6, 2:6) = xit;
yi(2:6, 2:6) = yit;

xi(1,:) = 1;
xi(7,:) = s(1);
yi(:,1) = 1;
yi(:,7) = s(2);
ideal(1, 1) = 1;
ideal(1, s(2)) = 1;
ideal(s(1), 1) = 1;
ideal(s(1), s(2)) = 1;

for k = 1:5
xi(k + 1, 1) = xi(k + 1, 2);
xi(k + 1, 7) = xi(k + 1, 2);
yi(1, k + 1) = yi(2, k + 1);
yi(7, k + 1) = yi(2, k + 1);
ideal(xi(k + 1, 2), 1) = 1;
ideal(1, yi(2, k + 1)) = 1;
ideal(xi(k + 1, 2), s(2)) = 1;
ideal(s(1), yi(2, k + 1)) = 1;
end

//scf(0);
//imshow(ideal);
//imwrite(ideal, 'idealgrid.bmp');

//scf(1);
//imshow(distort, []);
//xdyd = (locate(49, 1))';
//fprintfMat('xdyd.txt', xdyd);

xdyd = fscanfMat('xdyd.txt');

xd = s(1) - xdyd(:,2);
yd = xdyd(:,1);

xd = (matrix(xd', 7, 7))';
yd = (matrix(yd', 7, 7))';

newgrid_bilinear = zeros(s(1), s(2));
newgrid_nearest_neighbor = zeros(s(1), s(2));
for a = 1:6
for b = 1:6

vertex_upperleft = [xd(a, b), yd(a, b)];
vertex_upperright = [xd(a, b + 1), yd(a, b + 1)];
vertex_lowerleft = [xd(a + 1, b), yd(a + 1, b)];
vertex_lowerright = [xd(a + 1, b + 1), yd(a + 1, b + 1)];

xd4 = [vertex_upperleft(1); vertex_upperright(1); vertex_lowerleft(1); vertex_lowerright(1)];
yd4 = [vertex_upperleft(2); vertex_upperright(2); vertex_lowerleft(2); vertex_lowerright(2)];

T = [xi(a, b) yi(a, b) xi(a, b)*yi(a, b) 1; xi(a, b + 1) yi(a, b + 1) xi(a, b + 1)*yi(a, b + 1) 1; xi(a + 1, b) yi(a + 1, b) xi(a + 1, b)*yi(a + 1, b) 1; xi(a + 1, b + 1) yi(a + 1, b + 1) xi(a + 1, b + 1)*yi(a + 1, b + 1) 1];

C1to4 = inv(T)*xd4;
C5to8 = inv(T)*yd4;

for m = (xi(a, 1)):(xi((a + 1), 1))
for n = (yi(1, b)):(yi(1, (b + 1)))

points_in_one_box = [m n m*n 1];

xnew = points_in_one_box*C1to4;
ynew = points_in_one_box*C5to8;
rxnew = round(xnew);
rynew = round(ynew);

if xnew < 1 | xnew > s(1) | ynew < 1 | ynew > s(2)
newgrid_bilinear(m, n) = distort(m, n);
newgrid_nearest_neighbor(m, n) = distort(m, n);
else

if xnew - rxnew == 0 & ynew - rynew == 0
newgrid_bilinear(m, n) = distort(xnew, ynew);
else

nearest_lowerleft = [round(xnew - 0.5), round(ynew - 0.5)];
nearest_upperleft = [round(xnew - 0.5), round(ynew + 0.5)];
nearest_lowerright = [round(xnew + 0.5), round(ynew - 0.5)];
nearest_upperright = [round(xnew + 0.5), round(ynew + 0.5)];

nearest_pixels = [nearest_lowerleft(1) nearest_lowerleft(2) nearest_lowerleft(1)*nearest_lowerleft(2) 1; nearest_upperleft(1) nearest_upperleft(2) nearest_upperleft(1)*nearest_upperleft(2) 1; nearest_lowerright(1) nearest_lowerright(2) nearest_lowerright(1)*nearest_lowerright(2) 1; nearest_upperright(1) nearest_upperright(2) nearest_upperright(1)*nearest_upperright(2) 1];
distortgray_lowerleft = distort(nearest_lowerleft(1), nearest_lowerleft(2));
distortgray_upperleft = distort(nearest_upperleft(1), nearest_upperleft(2));
distortgray_lowerright = distort(nearest_lowerright(1), nearest_lowerright(2));
distortgray_upperright = distort(nearest_upperright(1), nearest_upperright(2));
distortgray_nearest = [distortgray_lowerleft; distortgray_upperleft; distortgray_lowerright; distortgray_upperright];

abcd_coefficients = inv(nearest_pixels)*distortgray_nearest;
interpolated_gray = [xnew ynew xnew*ynew 1]*abcd_coefficients;

newgrid_bilinear(m, n) = interpolated_gray;
newgrid_nearest_neighbor(m, n) = distort(rxnew, rynew);

end

end

end
end

end
end

//scf(2);
//imshow(newgrid_bilinear, []);
//imwrite(newgrid_bilinear/max(newgrid_bilinear), 'newgrid_bilinear.bmp');

//scf(3);
//imshow(newgrid_nearest_neighbor, []);
//imwrite(newgrid_nearest_neighbor/max(newgrid_nearest_neighbor), 'newgrid_nearest_neighbor.bmp');

Activity 12 - Color Image Segmentation

A region of interest (ROI) from a colored image is segmented in this activity using two types of segmentation - Parametric and Non-parametric.

The following image is searched from the internet.

Source: http://www.justfurfun.org/doghtml/yorikpage.htm

The blue ball which the dog holds is the ROI used for segmentation. A monochromatic patch is then cropped from the ROI and this is shown below.

This monochromatic patch is the basis of extracting the ROI from the whole image. Its normalized primary color channels red (R), green (G), and blue (B) separately with the whole image's are obtained next. This is done by dividing each color channel element-by-element to the sum of the RGB arrays resulting to the normalized chromaticity coordinates for red (r), green (g), and blue (b). The normalized chromaticity space is as follows.

Here, the 3 dimensional color space is reduced to only 2 having red as the horizontal axis and green as the vertical axis. Of course, blue has its region in the normalized chromaticity space since the relation between the normalized chromaticity coordinates is r + g + b = 1. Normalizing the color channels of the whole image and the patch of the ROI is very important because the shade or brightness of the colors of the whole image and the ROI is separated from their pure colors or chromaticities and so the image is segmented correctly.

Parametric segmentation is the first type implemented to the image. In this process, the probability of each pixel from the whole image belonging to the chromaticity of the ROI is determined through a Gaussian distribution having the form as shown below.

From the expressions above, sigma is the standard deviation of the normalized chromaticities of the patch of the ROI while mu is the mean. Then, r and g come from the normalized chromaticities of each pixel of the whole image. The segmented image is then generated from the multiplied or joint probabilities in the red and blue normalized channels. This is illustrated as follows.

Apparently, the white region represents the ROI that is the blue ball. Comparing from the original image with the blue ball, the image is well segmented since various shades of the ROI are indeed ignored and thus the whole blue ball is almost separated from the image.

Non-parametric segmentation operates in the probability distribution of the normalized chromaticity of the ROI alone without depending to a function such as the Gaussian distribution employed in the parametric segmentation. A 2 dimensional histogram is acquired here as shown below which is then verified from the normalized chromaticity space.

Both histograms above are comparable to the normalized chromaticity space, their bins are just varied for the sake of visualization (left histogram with 32 bins) and application of the histogram backprojection process (right histogram with 256 bins). The histogram agrees with the normalized chromaticity space since the peaks are located within the blue region knowing that the ROI has chromaticity within this area.
The histogram backprojection is where each pixel in the image is assigned to a value corresponding to the histogram value in the normalized chromaticity space. Hence, it is essential to increase the bins of the histogram to 256 in order to accommodate the 256 rounded integer values in the normalized chromaticity space. Finally, the result of the non-parametric segmentation is the following.

It can be observed that the image is not that well segmented compared to the parametric approach since majority of the blue ball particularly at the bottom part where its brightness is minimal is not extracted. The good thing about non-parametric segmentation is that no function is needed, instead, just the histogram of a monochromatic patch from the ROI is required. Therefore, for this case, a Gaussian function works great as basis of probability distribution for image segmentation.

Since I have successfully done and understand parametric and non-parametric segmentation of a colored image, I give myself 10/10 in this activity.

Throughout the activity, I have worked independently in its completion. However, I shared useful ideas that have helped my classmates.

Appendix
Below is the whole Scilab code utilized in this Activity.

stacksize(4e7);

image = imread('big_blue_ball.jpg');
I = imread('ROI.jpg');

R = I(:,:,1);
G = I(:,:,2);
B = I(:,:,3);

RGB = R + G + B;

r = R./RGB;
b = B./RGB;
g = G./RGB;

Ri = image(:,:,1);
Gi = image(:,:,2);
Bi = image(:,:,3);

RGBi = Ri + Gi + Bi;

ri = Ri./RGBi;
bi = Bi./RGBi;
gi = Gi./RGBi;

// Parametric Segmentation

rmean = mean(r);
gmean = mean(g);
rsigma = stdev(r);
gsigma = stdev(g);

rp = (1/(rsigma*sqrt(2*%pi)))*exp(-((ri - rmean).^2)/(2*rsigma^2));
gp = (1/(gsigma*sqrt(2*%pi)))*exp(-((gi - gmean).^2)/(2*gsigma^2));

rgp = round(rp.*gp);

//scf(0);
//imshow(rgp);
//imwrite(rgp, 'parametric segment.bmp');

// Non-parametric Segmentation
// 2D Histogram Plot

BINS = 256;
rint = round(r*(BINS - 1) + 1);
gint = round(g*(BINS - 1) + 1);
colors = gint(:) + (rint(:) - 1)*BINS;
hist = zeros(BINS, BINS);

for row = 1:BINS
for col = 1:(BINS - row + 1)
hist(row, col) = length(find(colors == (((col + (row - 1)*BINS)))));
end
end

histo = hist/max(hist);

//scf(1);
//mesh(histo);

// Backprojection

rib = ri*255;
gib = gi*255;

[a, b] = size(image);
segment = zeros(a, b);

for i = 1:a
for j = 1:b
c = round(rib(i, j)) + 1;
d = round(gib(i, j)) + 1;
segment(i, j) = hist(c, d);
end
end

//scf(2);
//imshow(segment);
//imwrite(segment, 'nonparametric segment.bmp');