This last activity is about demonstration of restoration of a corrupted grayscale image with a known degradation function which in this case is motion blur and additive noise using Weiner filtering.
The following schematic diagram is a model of the image degradation and restoration process.
From the diagram, f_hat(x, y) is the approximate original image after the degraded image passes through one or more restoration filters, then the degraded image in the spatial domain can then be written in an equation as follows.
Here, h(x, y) represents the degradation function, f(x, y) is the original image and n(x, y) embodies the added noise. Meanwhile, its frequency representation in Fourier space is shown below.
The transfer function of image degradation implemented here is the following.
The variable T corresponds to the duration of exposure while a and b are the blurring displacements in the horizontal or x and vertical or y direction respectively.
In restoring the original image, the estimate image f_hat and the corrupted image f must have minimum mean square error between them. This condition is satisfied through the expression as follows called the minimum mean square error filter or the Weiner filter.
Note that the power spectrum of the noise and the original image are included in the Weiner filter which are shown below.
The power spectrum is similar to the modulus of the degradation transfer function as in the following equation.
As usual the first factor in the right hand side of the expression above denotes the complex conjugate of H(u, v).
In most cases, the power spectrum of the noise and undergraded image are not known, hence the Weiner filter can be approximated in the expression as follows.
Instead of the power spectra, it is replaced by K which is a constant that can be varied.
At first, the following grayscale image is obtained from the internet.
Source: http://tvtropes.org/pmwiki/pmwiki.php/Main/Ptitlefjcz80qe
A Gaussian noise with mean and standard deviation of 0.02 is then applied to the image. Next, the degradation transfer function parameters a, b, and T are varied resulting to the set of images as shown below (Arranged from top to bottom, left to right).
For T = 1: (1) a = 0.1, b = 0.1; (2) a = 0.01, b = 0.01; (3) a = 0.001, b = 0.001
For a = 0.01, b = 0.01: (1) T = 0.01; (2) T = 0.1; (3) T = 10; (4) T = 100
For constant exposure time, it can be observed that the degraded image becomes more discernible as the blurring displacements a and b decrease. Meanwhile, for constant blurring displacements, the added Gaussian noise is masked by the blurred image as the exposure time T increases.
Shown as follows are the restored images using Weiner filtering with the spectrum of the noise and undergraded image for different degradation transfer function parameters (Arranged from top to bottom, left to right).
For T = 1: (1) a = 0.1, b = 0.1; (2) a = 0.01, b = 0.01; (3) a = 0.001, b = 0.001
For a = 0.01, b = 0.01: (1) T = 0.01; (2) T = 0.1; (3) T = 10; (4) T = 100
Apparently, the restoration approaches the original image as the blurring displacements decrease as well as the exposure time increases.
The following last set of images is composed of restored images using Weiner filter with varying K values (Arranged from top to bottom, left to right).
For a = 0.01, b = 0.01, T = 1: (1) K = 0; (2) K = 0.000001; (3) K = 0.00001; (4) K = 0.0001; (5) K = 0.001; (6) K = 0.01; (7) K = 0.1; (8) K = 1
It can be noticed that since a constant, which is based from the ratio of the power spectrum of the noise to the undergraded image, is added in all the elements of the matrix in the process Weiner filtering, the added Gaussian noise is eliminated at the same time magnifying the blurring effect as K increases.
Weiner filtering with the power spectrum of the noise and the undergraded image is then recommended to be used when the power spectrum of the added noise and the undergraded image is known and also with minimal degradation while Weiner filtering with the constant K is more applicable for various corrupted image even without the power spectra as long as K is carefully chosen.
Since I am able to demonstrate a corrupted image with motion blur and additive noise, and restore it using Weiner filtering successfully, I grade myself 10/10.
I have worked individually in this activity however I have shared my insights to my classmates.
Appendix
The Scilab code below is utilized in this activity.
stacksize(4e7);
image = gray_imread('dissidia.jpg');
//scf(0);
//imshow(image, []);
//imwrite(normal(image), 'bwdissidia.bmp');
s = size(image);
noise_gauss = grand(s(1), s(2), 'nor', 0.02, 0.02);
noisy_image = image + noise_gauss;
N = fft2(noise_gauss);
F = fft2(image);
a = 0.01;
b = 0.01;
T = 1;
H = [];
for i = 1:s(1)
for j = 1:s(2)
H(i, j) = (T/(%pi*(i*a + j*b)))*(sin(%pi*(i*a + j*b)))*exp(-%i*%pi*(i*a + j*b));
end
end
G = H.*F + N;
noisy_blurred = abs(ifft(G));
//scf(1);
//imshow(noisy_blurred, []);
//imwrite(normal(noisy_blurred), 'noisy blurred_a001_b001_T1.bmp');
SN = N.*conj(N);
SF = F.*conj(F);
restore1 = (((1)./H).*((H.*conj(H))./((H.*conj(H)) + (SN./SF)))).*G;
restore1 = abs(ifft(restore1));
//scf(2);
//imshow(restore1, []);
//imwrite(normal(restore1), 'restore_a001_b001_T1.bmp');
K = 0.01;
restore2 = (((1)./H).*((H.*conj(H))./((H.*conj(H)) + K))).*G;
restore2 = abs(ifft(restore2));
//scf(3);
//imshow(restore2, []);
//imwrite(normal(restore2), 'restoreK001.bmp');
The following schematic diagram is a model of the image degradation and restoration process.
From the diagram, f_hat(x, y) is the approximate original image after the degraded image passes through one or more restoration filters, then the degraded image in the spatial domain can then be written in an equation as follows.
Here, h(x, y) represents the degradation function, f(x, y) is the original image and n(x, y) embodies the added noise. Meanwhile, its frequency representation in Fourier space is shown below.
The transfer function of image degradation implemented here is the following.
The variable T corresponds to the duration of exposure while a and b are the blurring displacements in the horizontal or x and vertical or y direction respectively.
In restoring the original image, the estimate image f_hat and the corrupted image f must have minimum mean square error between them. This condition is satisfied through the expression as follows called the minimum mean square error filter or the Weiner filter.
Note that the power spectrum of the noise and the original image are included in the Weiner filter which are shown below.
The power spectrum is similar to the modulus of the degradation transfer function as in the following equation.
As usual the first factor in the right hand side of the expression above denotes the complex conjugate of H(u, v).
In most cases, the power spectrum of the noise and undergraded image are not known, hence the Weiner filter can be approximated in the expression as follows.
Instead of the power spectra, it is replaced by K which is a constant that can be varied.
At first, the following grayscale image is obtained from the internet.
Source: http://tvtropes.org/pmwiki/pmwiki.php/Main/Ptitlefjcz80qe
A Gaussian noise with mean and standard deviation of 0.02 is then applied to the image. Next, the degradation transfer function parameters a, b, and T are varied resulting to the set of images as shown below (Arranged from top to bottom, left to right).
For T = 1: (1) a = 0.1, b = 0.1; (2) a = 0.01, b = 0.01; (3) a = 0.001, b = 0.001
For a = 0.01, b = 0.01: (1) T = 0.01; (2) T = 0.1; (3) T = 10; (4) T = 100
For constant exposure time, it can be observed that the degraded image becomes more discernible as the blurring displacements a and b decrease. Meanwhile, for constant blurring displacements, the added Gaussian noise is masked by the blurred image as the exposure time T increases.
Shown as follows are the restored images using Weiner filtering with the spectrum of the noise and undergraded image for different degradation transfer function parameters (Arranged from top to bottom, left to right).
For T = 1: (1) a = 0.1, b = 0.1; (2) a = 0.01, b = 0.01; (3) a = 0.001, b = 0.001
For a = 0.01, b = 0.01: (1) T = 0.01; (2) T = 0.1; (3) T = 10; (4) T = 100
Apparently, the restoration approaches the original image as the blurring displacements decrease as well as the exposure time increases.
The following last set of images is composed of restored images using Weiner filter with varying K values (Arranged from top to bottom, left to right).
For a = 0.01, b = 0.01, T = 1: (1) K = 0; (2) K = 0.000001; (3) K = 0.00001; (4) K = 0.0001; (5) K = 0.001; (6) K = 0.01; (7) K = 0.1; (8) K = 1
It can be noticed that since a constant, which is based from the ratio of the power spectrum of the noise to the undergraded image, is added in all the elements of the matrix in the process Weiner filtering, the added Gaussian noise is eliminated at the same time magnifying the blurring effect as K increases.
Weiner filtering with the power spectrum of the noise and the undergraded image is then recommended to be used when the power spectrum of the added noise and the undergraded image is known and also with minimal degradation while Weiner filtering with the constant K is more applicable for various corrupted image even without the power spectra as long as K is carefully chosen.
Since I am able to demonstrate a corrupted image with motion blur and additive noise, and restore it using Weiner filtering successfully, I grade myself 10/10.
I have worked individually in this activity however I have shared my insights to my classmates.
Appendix
The Scilab code below is utilized in this activity.
stacksize(4e7);
image = gray_imread('dissidia.jpg');
//scf(0);
//imshow(image, []);
//imwrite(normal(image), 'bwdissidia.bmp');
s = size(image);
noise_gauss = grand(s(1), s(2), 'nor', 0.02, 0.02);
noisy_image = image + noise_gauss;
N = fft2(noise_gauss);
F = fft2(image);
a = 0.01;
b = 0.01;
T = 1;
H = [];
for i = 1:s(1)
for j = 1:s(2)
H(i, j) = (T/(%pi*(i*a + j*b)))*(sin(%pi*(i*a + j*b)))*exp(-%i*%pi*(i*a + j*b));
end
end
G = H.*F + N;
noisy_blurred = abs(ifft(G));
//scf(1);
//imshow(noisy_blurred, []);
//imwrite(normal(noisy_blurred), 'noisy blurred_a001_b001_T1.bmp');
SN = N.*conj(N);
SF = F.*conj(F);
restore1 = (((1)./H).*((H.*conj(H))./((H.*conj(H)) + (SN./SF)))).*G;
restore1 = abs(ifft(restore1));
//scf(2);
//imshow(restore1, []);
//imwrite(normal(restore1), 'restore_a001_b001_T1.bmp');
K = 0.01;
restore2 = (((1)./H).*((H.*conj(H))./((H.*conj(H)) + K))).*G;
restore2 = abs(ifft(restore2));
//scf(3);
//imshow(restore2, []);
//imwrite(normal(restore2), 'restoreK001.bmp');




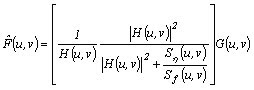


























No comments:
Post a Comment